Quella del genitore troppo orgoglioso del propri figli è una figura che è piuttosto semplice incontrare, tanto quanto spero siano rare le figure opposte. Io appartengo alla prima categoria, ovviamente con la certezza di averne buone ragioni.
Tuttavia è proprio per questo che ho fatto un po’ fatica a decidere di pubblicare questo post – ma infine, superate queste resistenze, eccolo. Vi confesso che all’inizio avevo pensato di esercitarmi nella classica “lettera a mio figlio”, ma non ho voluto esagerare: certe cose è giusto che restino un fatto privato.
Ivan ha appena superato l’esame di maturità scientifica. Per questo, ha dovuto anche fare una tesina, alla quale ha dato il titolo Le geometrie non euclidee. In caso voleste leggerla tutta, la potete scaricare in pdf a questo link.
Quando l’ho letta per la prima volta mi sono commosso, per la qualità delle cose che diceva. In particolare, appena ho letto la parte conclusiva ho pensato che questa non parlava solo di matematica – parlava di cose che ci riguardano tutti. Per questo, ho chiesto a Ivan il permesso di condividerla con voi, e Ivan con un sorriso ha detto “va bene”.
Non voglio commentare questo brano, perché si commenta da solo, ma mi rivolgo a Ivan con un solo frammento di quello che avrei potuto scrivergli, per ringraziarlo – concedetemelo.
Caro Ivan, un grandissimo fotografo che non conosci, Robert Adams, ha detto di non poter dedicare più del cinque per cento del suo tempo alla vera ragione per cui ama la fotografia – ossia essere sul campo a fotografare. Credo che ogni attività che facciamo, compreso amare, sia sempre travolta da un novantacinque per cento di necessità quotidiane, difficoltà, distrazioni, impegni collegati (a volte bellissimi, a volte meno, a volte solo routine) e così via.
Nel caso di quello che faccio, lo vedi, oltre al poco fotografare bisogna anche passare ormai molto tempo al computer, coltivare relazioni, parlare con gli stampatori e i corniciai, frequentare altri artisti e curatori, insegnare, giostrare coi commercialisti, pagare tasse, inseguire i pagamenti in ritardo, studiare sempre, sperimentare… una immensa quantità di cose, leggere e pesanti, che a volte arrivano quasi ad offuscare la vera ragione, appunto, per cui facciamo quello che facciamo.
Ma senza quel cinque per cento il resto non avrebbe senso, o ne avrebbe talmente poco da condannarci a una vita amara.
Ecco Ivan, ti dico solo questo: proteggi il tuo cinque per cento. Nella vita incontrerai soprattutto persone e situazioni che, magari senza rendersene conto, faranno di tutto per togliertelo, per spegnerlo – ma ci sarà anche chi capirà, ci saranno anche momenti bellissimi. Proteggi il tuo amore, fallo crescere e fallo vedere: solo così proteggerai la bellezza e la ricchezza della tua vita.
Ivan Andreoni, Le geometrie non euclidee, estratto dalle Conclusioni:
[…]
La matematica e la filosofia, fra gli studenti, sono le due discipline che si contendono il primato del “quando mai mi servirà ‘sta roba nella vita”. Riguardo la filosofia, si espresse nel ‘68 Gustavo Bontadini, affermando provocatoriamente che la filosofia non serve a nulla, mentre le scienze servono, servono il potere: la filosofia dunque, nella sua inutilità, è l’unico sapere veramente libero. La scienza è infatti per eccellenza quella disciplina utile che, anche nei suoi aspetti più teorici, ha un immediato rapporto con la tecnica e la praticità (per esempio, le trasmissioni satellitari non funzionerebbero senza effettuare aggiustamenti sugli orologi calcolati usando la relatività generale, settore apparentemente troppo teorico per avere un ruolo pratico nella vita comune).
La matematica, a mio avviso, si colloca a metà fra scienza e filosofia. Questa ha in comune con la scienza un metodo rigoroso che, come scrisse Nietzsche, “aiuta a diradare le nebbie della metafisica”. Ma mentre la scienza è una disciplina empirica, legata dunque al mondo materiale, in continua revisione, la matematica è più intellettuale, fondata su assiomi precisi, dedotta con teoremi che conferiscono un grado di certezza e precisione ben superiore. Per questo motivo, molti filosofi hanno considerato la matematica come ‘scienza per eccellenza’: i Pitagorici vedevano i numeri molto legati alla verità, Platone considerava le idee legate ai numeri, e nella filosofia più moderna molti furono i filosofi-matematici che diedero contributi a entrambe le discipline (Cartesio e Leibniz sono due fra questi).
La matematica condivide con la filosofia un approccio teorico e dunque un’inutilità apparente, non avendo un immediato riscontro pratico. Ma la matematica, così come la filosofia, dalla sua inutilità trae vantaggio, perché è proprio questo che le consente una libertà nella ricerca della bellezza o di altri valori.
Così la pensava il matematico inglese Godfrey Harold Hardy (1877-1947), che espresse il suo pensiero in A Mathematician’s Apology (1940): “I have never done anything ‘useful’. No discovery of mine has made, or is likely to make, directly or indirectly, for good or ill, the least difference to the amenity of the world”.
Va specificato che Hardy si colloca in un contesto in cui alcune teorie matematiche avevano avuto recente applicazione bellica: fu probabilmente anche l’orrore della prima guerra mondiale, in cui si videro le peggiori applicazioni della scienza, a far preferire a molti pensatori l’approccio più puro e teorico possibile.
Ma anche la matematica pura è destinata a diventare matematica applicata, prima o poi: per fare alcuni esempi, i numeri complessi furono menzionati per la prima volta da Girolamo Cardano nel XVI secolo come artificio per poter applicare le ‘formule di Cardano’ nella risoluzione delle equazioni di terzo grado. Oggi i numeri complessi hanno applicazioni in molti campi, fra cui la meccanica quantistica e l’ingegneria elettronica. I numeri primi, uno degli aspetti più misteriosi e affascinanti della teoria dei numeri, che furono studiati e sono tuttora studiati da numerosi matematici (fra cui lo stesso Hardy), svolgono oggi un ruolo centrale nella crittografia.
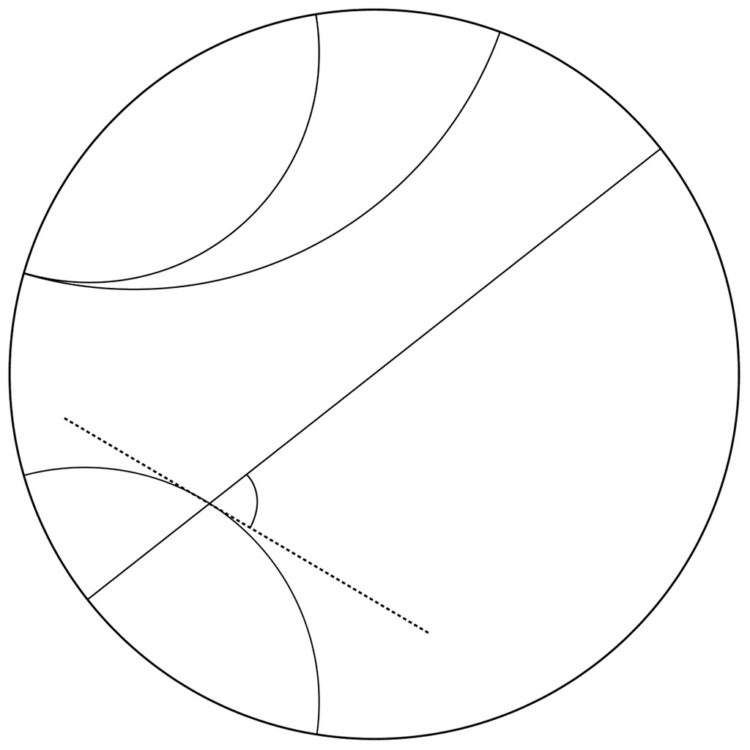
Le geometrie non euclidee sono un altro eccellente esempio di ciò: quando Lobačevskij e Bolyai decisero di analizzare approfonditamente il sistema anti intuitivo in cui la parallela non è unica, difficilmente avrebbero immaginato che i loro studi sarebbero stati applicati alla fisica.
È questo il motivo per cui trovo la matematica estremamente affascinante: da una parte, è una disciplina teorica e pura, e per questo dotata di un particolare fascino; dall’altra, è rigorosa e precisa, e le sue inevitabili ma imprevedibili applicazioni la rendono utile senza comprometterne la fondamentale bellezza.